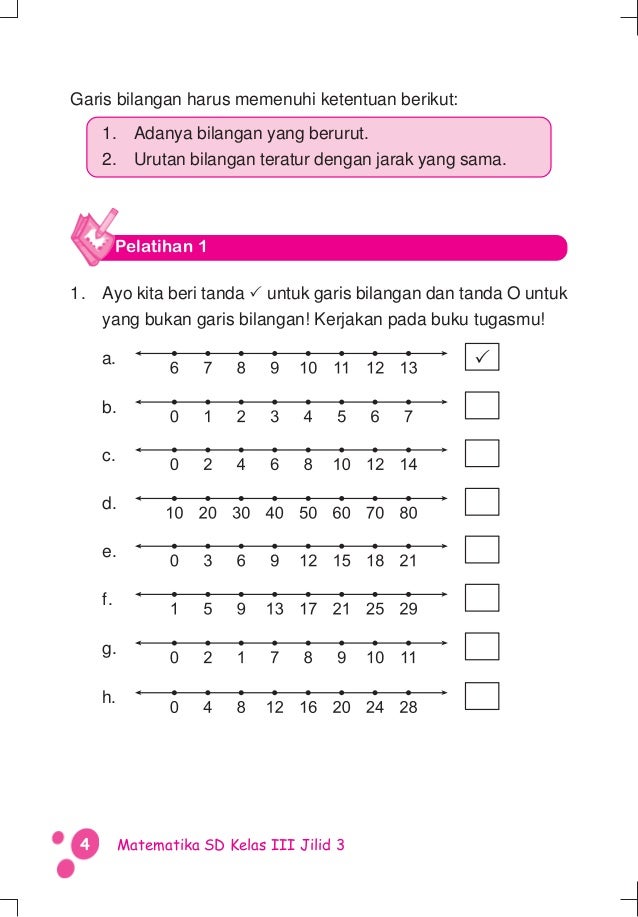
Memahami Pecahan di Kelas 3 dengan Garis Bilangan

Pendahuluan

Pecahan adalah konsep matematika dasar yang sangat penting. Pemahaman yang kuat tentang pecahan di kelas 3 akan menjadi fondasi yang kokoh untuk pembelajaran matematika yang lebih kompleks di masa depan. Salah satu cara efektif untuk memperkenalkan dan memvisualisasikan pecahan kepada siswa kelas 3 adalah dengan menggunakan garis bilangan. Garis bilangan membantu siswa memahami konsep pecahan secara visual, membandingkan pecahan, dan melakukan operasi sederhana dengan pecahan.

Artikel ini akan membahas secara mendalam tentang bagaimana menggunakan garis bilangan untuk mengajarkan pecahan di kelas 3, dilengkapi dengan contoh soal dan pembahasan yang mudah dipahami.

Outline Artikel

1. Apa itu Pecahan?
   • Definisi pecahan
   • Bagian-bagian pecahan: pembilang dan penyebut
   • Representasi pecahan dalam kehidupan sehari-hari
2. Mengapa Garis Bilangan Penting untuk Memahami Pecahan?
   • Visualisasi konsep pecahan
   • Membandingkan pecahan dengan mudah
   • Memahami hubungan antar pecahan
3. Cara Membuat dan Menggunakan Garis Bilangan untuk Pecahan
   • Membuat garis bilangan dasar
   • Membagi garis bilangan menjadi beberapa bagian yang sama
   • Menandai pecahan pada garis bilangan
4. Contoh Soal Pecahan Kelas 3 dengan Garis Bilangan
   • Soal 1: Menentukan pecahan pada garis bilangan
   • Soal 2: Membandingkan dua pecahan
   • Soal 3: Menemukan pecahan yang senilai
   • Soal 4: Menjumlahkan pecahan dengan penyebut yang sama
   • Soal 5: Mengurangkan pecahan dengan penyebut yang sama
5. Tips Mengajar Pecahan dengan Garis Bilangan kepada Siswa Kelas 3
   • Gunakan benda-benda konkret sebagai representasi
   • Buat garis bilangan yang besar dan mudah dilihat
   • Gunakan warna untuk membedakan pecahan
   • Libatkan siswa secara aktif dalam proses pembelajaran
   • Berikan latihan yang bervariasi
6. Kesalahan Umum dalam Memahami Pecahan dan Cara Mengatasinya
   • Kesalahan: Membingungkan pembilang dan penyebut
   • Kesalahan: Tidak memahami konsep "bagian yang sama"
   • Kesalahan: Sulit membandingkan pecahan dengan penyebut berbeda
7. Aplikasi Pecahan dalam Kehidupan Sehari-hari
   • Membagi makanan
   • Mengukur bahan masakan
   • Menentukan waktu
8. Kesimpulan

Isi Artikel

1. Apa itu Pecahan?

Pecahan adalah bilangan yang merepresentasikan sebagian dari keseluruhan. Dalam matematika, pecahan ditulis dalam bentuk a/b, di mana ‘a’ disebut pembilang dan ‘b’ disebut penyebut.

• Pembilang (a): Menunjukkan berapa banyak bagian yang diambil atau diperhatikan dari keseluruhan.
• Penyebut (b): Menunjukkan berapa banyak bagian yang sama yang membentuk keseluruhan.

Contoh: Jika kita memotong sebuah pizza menjadi 4 bagian yang sama, dan kita mengambil 1 potong, maka kita telah mengambil 1/4 (satu per empat) dari pizza tersebut. Di sini, 1 adalah pembilang dan 4 adalah penyebut.

Dalam kehidupan sehari-hari, kita sering menggunakan pecahan tanpa menyadarinya. Contohnya, "setengah jam," "seperempat kue," atau "tiga perempat gelas air."

2. Mengapa Garis Bilangan Penting untuk Memahami Pecahan?

Garis bilangan adalah alat bantu visual yang sangat efektif untuk membantu siswa kelas 3 memahami konsep pecahan. Berikut adalah beberapa alasan mengapa garis bilangan penting:

• Visualisasi Konsep Pecahan: Garis bilangan memberikan representasi visual yang jelas tentang pecahan. Siswa dapat melihat pecahan sebagai titik atau interval pada garis, yang membantu mereka memahami bahwa pecahan mewakili sebagian dari keseluruhan.
• Membandingkan Pecahan dengan Mudah: Dengan menempatkan pecahan pada garis bilangan, siswa dapat dengan mudah membandingkan nilai pecahan. Pecahan yang terletak lebih jauh ke kanan pada garis bilangan memiliki nilai yang lebih besar.
• Memahami Hubungan Antar Pecahan: Garis bilangan membantu siswa memahami hubungan antara pecahan yang berbeda, seperti pecahan senilai (ekivalen) atau pecahan yang lebih besar atau lebih kecil dari pecahan lainnya.

3. Cara Membuat dan Menggunakan Garis Bilangan untuk Pecahan

Berikut adalah langkah-langkah untuk membuat dan menggunakan garis bilangan untuk pecahan:

• Membuat Garis Bilangan Dasar:
  • Gambarkan sebuah garis lurus horizontal.
  • Tandai titik awal garis dengan angka 0 (nol) dan titik akhir garis dengan angka 1 (satu). Angka 0 mewakili "tidak ada" dan angka 1 mewakili "keseluruhan."
• Membagi Garis Bilangan menjadi Beberapa Bagian yang Sama:
  • Tentukan penyebut pecahan yang ingin direpresentasikan. Misalnya, jika kita ingin merepresentasikan pecahan dengan penyebut 4, kita perlu membagi garis bilangan menjadi 4 bagian yang sama.
  • Gunakan penggaris atau perkiraan visual untuk membagi garis bilangan menjadi bagian-bagian yang sama. Pastikan setiap bagian memiliki panjang yang sama.
• Menandai Pecahan pada Garis Bilangan:
  • Mulai dari titik 0, hitung jumlah bagian yang sesuai dengan pembilang pecahan.
  • Tandai titik tersebut pada garis bilangan dan tuliskan pecahan di atasnya.

Contoh: Untuk menandai pecahan 3/4 pada garis bilangan, kita bagi garis bilangan antara 0 dan 1 menjadi 4 bagian yang sama. Kemudian, kita hitung 3 bagian dari titik 0 dan menandai titik tersebut dengan pecahan 3/4.

4. Contoh Soal Pecahan Kelas 3 dengan Garis Bilangan

Berikut adalah beberapa contoh soal pecahan kelas 3 yang dapat diselesaikan dengan menggunakan garis bilangan:

• Soal 1: Menentukan pecahan pada garis bilangan

  • Soal: Tentukan pecahan yang ditunjukkan oleh titik A pada garis bilangan berikut:

    (Gambar garis bilangan dengan titik A di antara 0 dan 1, dibagi menjadi 5 bagian yang sama, dan titik A berada di bagian ke-2 setelah 0)

  • Pembahasan: Garis bilangan dibagi menjadi 5 bagian yang sama, sehingga penyebutnya adalah 5. Titik A berada di bagian ke-2 setelah 0, sehingga pembilangnya adalah 2. Jadi, pecahan yang ditunjukkan oleh titik A adalah 2/5.

• Soal 2: Membandingkan dua pecahan

  • Soal: Manakah yang lebih besar, 1/3 atau 2/3? Gunakan garis bilangan untuk menjelaskannya.

    (Gambar garis bilangan dengan pecahan 1/3 dan 2/3 ditandai)

  • Pembahasan: Pada garis bilangan, 2/3 terletak lebih jauh ke kanan daripada 1/3. Ini berarti 2/3 lebih besar dari 1/3.

• Soal 3: Menemukan pecahan yang senilai

  • Soal: Tentukan pecahan yang senilai dengan 1/2. Gunakan garis bilangan untuk menjelaskannya.

    (Gambar garis bilangan dengan pecahan 1/2, 2/4, dan 3/6 ditandai)

  • Pembahasan: Jika kita membagi garis bilangan menjadi 2 bagian yang sama, 4 bagian yang sama, dan 6 bagian yang sama, kita akan melihat bahwa 1/2, 2/4, dan 3/6 menempati posisi yang sama pada garis bilangan. Ini berarti mereka adalah pecahan yang senilai.

• Soal 4: Menjumlahkan pecahan dengan penyebut yang sama

  • Soal: Hitung 1/4 + 2/4. Gunakan garis bilangan untuk menjelaskannya.

    (Gambar garis bilangan dengan penjumlahan 1/4 + 2/4 diilustrasikan)

  • Pembahasan: Mulai dari 0, bergerak sejauh 1/4 ke kanan. Kemudian, bergerak lagi sejauh 2/4 ke kanan. Kita akan sampai di titik 3/4. Jadi, 1/4 + 2/4 = 3/4.

• Soal 5: Mengurangkan pecahan dengan penyebut yang sama

  • Soal: Hitung 3/5 – 1/5. Gunakan garis bilangan untuk menjelaskannya.

    (Gambar garis bilangan dengan pengurangan 3/5 – 1/5 diilustrasikan)

  • Pembahasan: Mulai dari 0, bergerak sejauh 3/5 ke kanan. Kemudian, bergerak sejauh 1/5 ke kiri. Kita akan sampai di titik 2/5. Jadi, 3/5 – 1/5 = 2/5.

5. Tips Mengajar Pecahan dengan Garis Bilangan kepada Siswa Kelas 3

• Gunakan Benda-Benda Konkret sebagai Representasi: Sebelum menggunakan garis bilangan, bantu siswa memahami konsep pecahan dengan menggunakan benda-benda konkret seperti pizza, kue, atau kertas yang dipotong-potong.
• Buat Garis Bilangan yang Besar dan Mudah Dilihat: Gunakan papan tulis atau kertas besar untuk membuat garis bilangan yang mudah dilihat oleh seluruh siswa di kelas.
• Gunakan Warna untuk Membedakan Pecahan: Gunakan warna yang berbeda untuk menandai pecahan yang berbeda pada garis bilangan. Ini akan membantu siswa membedakan dan membandingkan pecahan dengan lebih mudah.
• Libatkan Siswa Secara Aktif dalam Proses Pembelajaran: Ajak siswa untuk membuat garis bilangan sendiri, menandai pecahan, dan menyelesaikan soal-soal pecahan dengan menggunakan garis bilangan.
• Berikan Latihan yang Bervariasi: Berikan soal-soal latihan yang bervariasi untuk membantu siswa memahami konsep pecahan dengan lebih baik.

6. Kesalahan Umum dalam Memahami Pecahan dan Cara Mengatasinya

• Kesalahan: Membingungkan Pembilang dan Penyebut: Siswa seringkali tertukar antara pembilang dan penyebut. Untuk mengatasi hal ini, selalu tekankan bahwa penyebut menunjukkan jumlah total bagian yang sama, sedangkan pembilang menunjukkan jumlah bagian yang diperhatikan.
• Kesalahan: Tidak Memahami Konsep "Bagian yang Sama": Siswa mungkin tidak memahami bahwa pecahan hanya berlaku jika keseluruhan dibagi menjadi bagian-bagian yang sama. Tekankan pentingnya bagian yang sama dalam definisi pecahan.
• Kesalahan: Sulit Membandingkan Pecahan dengan Penyebut Berbeda: Siswa seringkali kesulitan membandingkan pecahan dengan penyebut berbeda. Ajarkan mereka cara mencari pecahan senilai dengan penyebut yang sama sebelum membandingkan.

7. Aplikasi Pecahan dalam Kehidupan Sehari-hari

Pecahan memiliki banyak aplikasi dalam kehidupan sehari-hari. Berikut adalah beberapa contoh:

• Membagi Makanan: Membagi pizza, kue, atau buah-buahan kepada teman atau anggota keluarga.
• Mengukur Bahan Masakan: Menggunakan takaran 1/2 sendok teh, 1/4 cangkir, atau 3/4 gelas dalam resep masakan.
• Menentukan Waktu: Memahami konsep "setengah jam," "seperempat jam," atau "tiga perempat jam."

8. Kesimpulan

Memahami pecahan adalah keterampilan matematika yang penting bagi siswa kelas 3. Garis bilangan adalah alat bantu visual yang efektif untuk membantu siswa memahami konsep pecahan, membandingkan pecahan, dan melakukan operasi sederhana dengan pecahan. Dengan menggunakan garis bilangan dan metode pengajaran yang tepat, guru dapat membantu siswa kelas 3 membangun fondasi yang kuat dalam pemahaman pecahan.